Top > Research > ゲーム理論的観点からのネットワーク設計
■ ゲーム理論的観点からのネットワーク設計
1. 利己的ルーティング
ゲーム理論では、 各プレーヤーは全体の利益よりも 自身の利益を最大化しようとして行動することが前提とされます。 自分が損をするとみるやプレーヤーは行動を修正し、 その結果ゲームの状況はある均衡点(ナッシュ均衡)に収束することが知られています。
車のドライバーは典型的なゲーム理論的プレーヤーで、 自分が早く目的地に着けるように空いている道を選んで走りますが、 他の車の利益を考えて道を選ぶようなことはしません。 このような経路選択ポリシーは利己的ルーティングと呼ばれます。 インターネットも 動的ルーティングポリシーには利己的ルーティングが採用されています。
2. Braessのパラドックス
利己的ルーティングの下では、不思議な現象が起こり得ることが知られています。 道路を増やして車の流れが良くなることがあっても悪くなることはないと、普通は 考えます。 次の図はこのことが成立しないケースを示す例で、 Braessのパラドックスと呼ばれています。
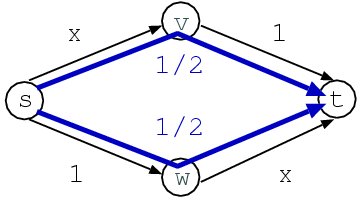
Braessのパラドックス(その1)
sからtへ総量1の車が向かうとします。 また、道s→tとw→tについては通過した車の量に比例した時間がかかり、 s→wとv→tについては常に1時間がかかる (太い道路で、所要時間が通行量に左右されないと考えます)とします。 上の図はこの条件での均衡点を示しており、 所要時間は1/2+1=3/2時間です。
さて、もしv→wに所要時間0の非常に太くて短い道路が 追加されたらどうなるでしょうか。
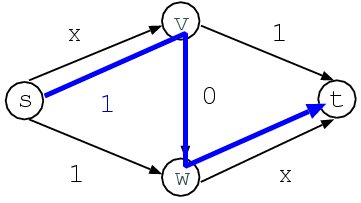
Braessのパラドックス(その2)
均衡点は図のように変化し、結果として所要時間は1+1=2時間に増えます。 追加された道が車をミスリードしたわけです。
3. 研究課題
利己的ルーティングを採用するネットワークには 通信をミスリードするリンクがあり得ます。 そのようなリンクは作るべきではないし、知らずに作ってしまっていたとしたら 見つけて撤去するべきです。 ところが、すでにあるネットワークからミスリードするリンクを検出することは、 一般にはNP困難(簡単ではなさそうということ)であることが知られています。 当研究室では、検出が容易なネットワークにはどのようなものがあるか 調べています。